C++求解一元多次方程组

不希望图标闪现到固定位置，又不想直线移动过去，那怎么办呢？

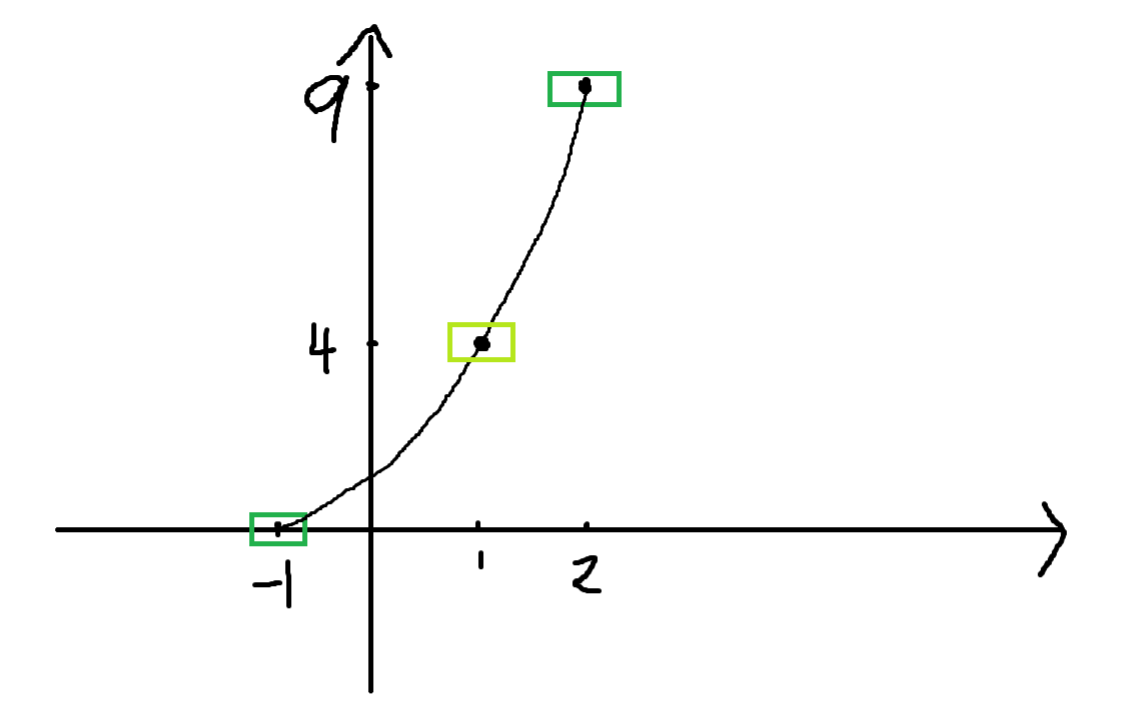
曲线移动就需要求解曲线方程，以下面一个场景为例：将方块从初始坐标以抛物线的方式移动到目标坐标，任意选择一个抛物线经过的第三个点，来求解方程 y=a*x^2+b*x+c。

绿色矩形从(-1,0)移动到(2,9)，路途中我们任意选取一点，为方便计算选取(1,4)。

多项式求解一元n次方程

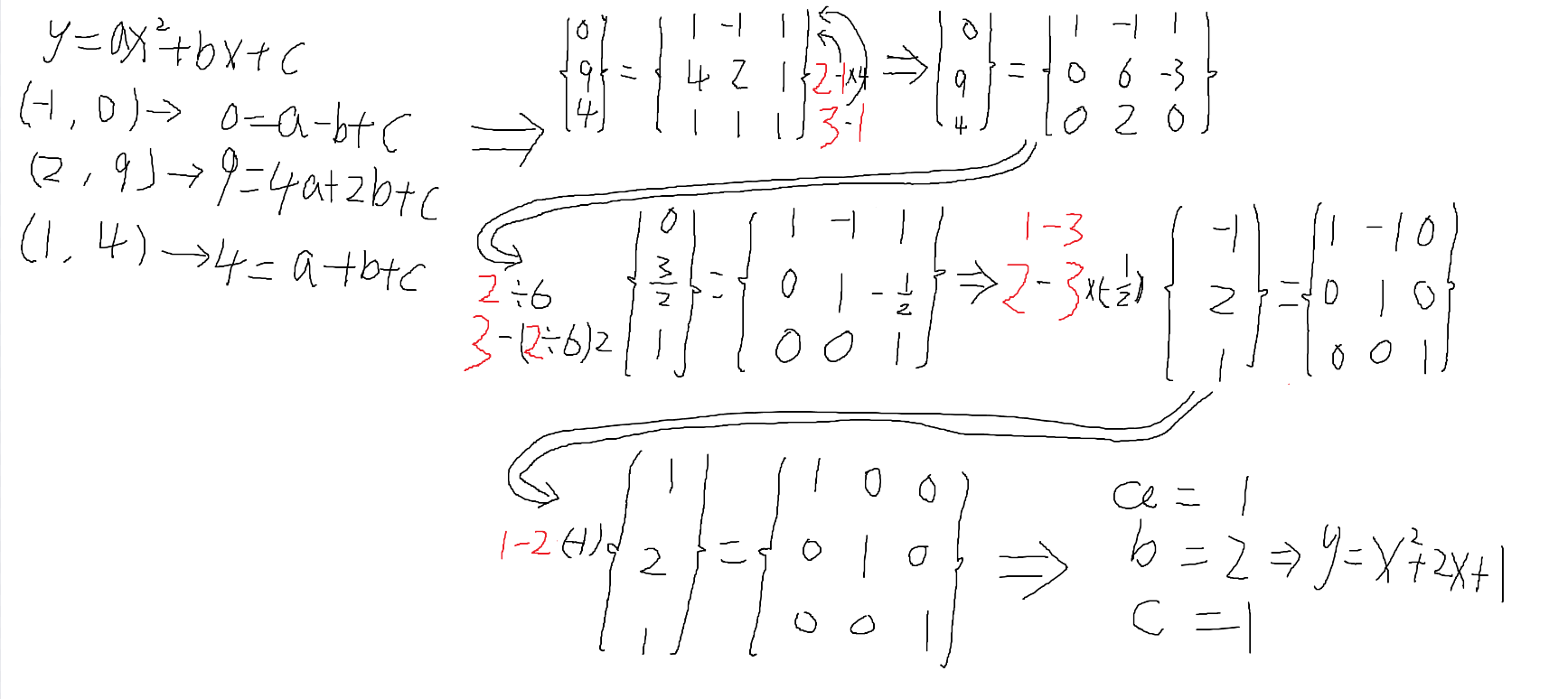
将三个点带入方程得到三个等式，(-1,0)，(2,9)，(1,4)，如果你学过离散数学，利用多项式求解方程，那么下面的求解过程你一定很熟悉。其主要思想是：

• 第一步列出等式矩阵；

• 第二步：将等式化简为“上三角矩阵”，对角线全部为1；

• 第三步将矩阵化简为“对角矩阵”。

此时方程的解即为y值矩阵的值。

代码求解n次方程

方程传入三个参数，分别是对应的横坐标数组，纵坐标数组，和方程的次数。

参数要求数组长度大于等于方程次数+1时才能求解方程。

vector<double> solutionFunction(vector<double> x, vector<double> y, int n) {
	vector<double> a;
	if (x.size() <= n || y.size() <= n || n <= 0) {
		return a;
	}
	double* sx = (double*)calloc((n + 1) * (n + 1), sizeof(double));
	double* sy = (double*)calloc(n + 1, sizeof(double));
	//列出方程多项式
	for (int i = 0; i <= n; i++) {
		sx[i * (n + 1) + 0] = 1;
		sy[i] = y[i];
		for (int j = 1; j <= n; j++) {
			sx[i * (n + 1) + j] = sx[i * (n + 1) + j - 1] * x[i];
		}
	}
    //将方程化简为上三角矩阵
	for (int i = 0; i <= n; i++) {
		//double x2 = sx[i*(n + 1) + i];
		sy[i] /= sx[i * (n + 1) + i];
		for (int k = n; k >= i; k--) {
			sx[i * (n + 1) + k] /= sx[i * (n + 1) + i];
		}
		for (int j = i + 1; j <= n; j++) {
			double m = sx[j * (n + 1) + i];
			sy[j] -= sy[i] * m;
			for (int k = 0; k <= n; k++) {
				sx[j * (n + 1) + k] -= sx[i * (n + 1) + k] * m;
			}
		}
	}
	//将方程化简为对角矩阵
	for (int i = n; i >= 0; i--) {
		sy[i] /= sx[i * (n + 1) + i];
		sx[i * (n + 1) + i] /= sx[i * (n + 1) + i];
		for (int j = i - 1; j >= 0; j--) {
			sy[j] -= sy[i] * sx[j * (n + 1) + i];
			sx[j * (n + 1) + i] -= sx[i * (n + 1) + i] * sx[j * (n + 1) + i];
		}
	}
	//返回方程的解
	for (int i = 0; i <= n; i++) {
		a.push_back(sy[i]);
	}
	free(sy);
	free(sx);
	return a;
}

题外篇

上面求解出来的方程只会经过需要的三个点，但其运行轨迹可能是与预想的不一样。如图求解出的方程以黑色线条运行，但黑色线条超出了中间点的坐标范围（容易超出屏幕），那这种情况怎么办呢？

要想在中间点位置处于最高或最低点，那就要用到导数的概念了，当导数等于0时为方程的极值点，利用左右两个点加上中间点横坐标导数等于0组成三个方程，这样就能以中间点的横坐标作为最低或者最高点，但是这样又会出现新的问题，中间点的纵坐标可能超出范围。

那么将方程分为两个，左边和右边都在中间点处去的极值又会是什么样的情况呢？